
Many concepts in mathematics are readily understood in terms of simple illustrations, which may point the way toward rigorous (symbolic) proofs. This is particularly so in the case of geometry. However, even non-geometrical concepts such as topological relationships can also benefit from idiomatic graphical representations. Let us consider a simple theorem from real analysis that rests upon purely metric and topological notions and explore a hypothetical proof procedure that is guided by iconic representations.
Suppose that we wish to prove a totally bounded set S is also relatively compact. A "totally bounded" set is one that can be "covered" by a finite number of open balls (think of them as "disks" ) of any given diameter. While all sets of finite extent have this property in a simple Euclidean space, the situation is more interesting in infinite-dimensional spaces (such as collections of functions). Fortunately, even collections of infinite-dimensional functions can often be reasoned about as though they were points on a plane, as this example will show. A "relatively compact" set is one in which any infinite sequence of points (or functions) has a Cauchy subsequence; that is, a subset whose points eventually cluster together within an arbitrarily small region (essentially "converging" to a single point). Both concepts are meaningful in any metric topology, and involve essentially no geometry at all.
To prove the assertion it is sufficient to show that any infinite sequence in a totally bounded set must contain a Cauchy sequence (and thus its closure is compact). To produce a proof, we must somehow make use of the fact that the set is totally bounded to extract a Cauchy sequence from an arbitrary infinite sequence in the set. This can be done using a familiar iterative construction with a clear visual metaphor that occurs repeatedly in analysis.
Figure 2 shows a sequence of illustrations similar to what one might draw in attempting to find the desired connection; such illustrations are very common in analysis, and they lend themselves to random construction by computer. One implication of total boundedness is that we may obtain an open cover consisting of a finite number of e-balls, represented iconically as circles. (In proofs of this nature shape is irrelevant.) These balls may also be chosen by the computer in response to a user specifying the desired e, perhaps by drawing the first of the e-balls. The key to the proof is in utilizing the finiteness of the cover; since the sequence is infinite, it must hit at least one of the e-balls in the cover "infinitely often," which is another common idiom of analysis that can be given a visual representation. In the illustration, the e-balls hit infinitely often are simply shaded. To aid the user in avoiding incorrect assumptions, the "arbitrary" examples generated by the computer should contain reminders of valid special cases, such as a single point being visited infinitely many times.
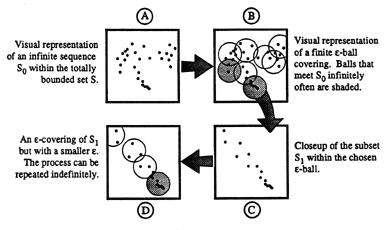 |
|
|
By repeating this construction several times, it becomes evident that it can be repeated indefinitely, since the subsequences chosen by this process retain the essential properties of the original sequence. That is, the properties of the subsequence are invariant under the iteration. See Figure 3. Verifying this symbolically leads to a rigorous proof Another fact that the system might provide a visual hint of is that the construction does not ensure strictly nested s-balls, which may require special care in some constructions, although it causes no difficulty in this example. See the right-hand side of Figure 3.
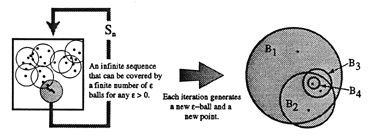 |
|
|
This example illustrates the potential for diagrammatic interaction in exploring topological concepts. The role of the diagram is to serve as a guide for the mathematics, not a substitute for it. Once the underlying principles are discovered, symbolic methods can be used to construct the proof. While diagrams may also form the basis of rigorous proofs, such approaches will not be emphasized in this work.
The study of abstract machines provides another interesting opportunity for exploring new forms of human-computer interaction. For example, finite automata lend themselves particularly well to diagrammatic representations, which are isomorphic to their formal definitions and amenable to gestural manipulation. Traditionally, these representations have been difficult to use in all but trivial cases, where the transition diagrams can be drawn by hand and the machine simulated mentally. By allowing such a diagram to be directly specified and manipulated via gestural interaction, the representation would become a far more useful tool, especially in the classroom. A student project is currently under way to develop a prototype of such a system, which is targeted to be used in teaching an introductory course in computer science theory at Caltech in the fall of 1997.
 |
|
|
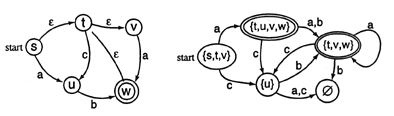
To illustrate, consider the state transition diagram shown on the left of Figure 4. This diagram could be constructed using only five types of gestures corresponding roughly to the five formal components of a finite automaton: state, arrow, start, final, and label. Other operations that could be effected gesturally include adding and removing components, changing the layout, running the machine on a given string, and transforming it into another form, such as changing a non-deterministic machine into a deterministic one (See Figure 4). Other fundamental concepts of computer science that will be considered for gestural interaction include grammars, predicate calculus, stepwise refinement of programs, and recursive function theory.
| Home | Research | Outreach | Televideo | Admin | Education |